Análisis Matemático (Fourier)

En ciertos equipos electrónicos -en especial los convertidores estáticos de potencia- se presentan formas de onda del tipo no-sinusoidal periódicas para sus señales de corriente y/o tensión (principalmente las de entrada), las cuales son difíciles de representar a través de una ecuación matemática. Esto lleva a utilizar la herramienta matemática llamada Series Trigonométricas de Fourier, que tiene la característica de representar cualquier señal periódica como una suma (superposición) de funciones sinusoidales. Conocer las amplitudes de cada función sinusoidal (coeficientes de Fourier o magnitudes armónicas) es de gran importancia y utilidad en el diseño de convertidores estáticos de potencia, ya que se puede saber con certeza los problemas que puede provocar cada equipo. Además, se puede determinar los niveles del contenido armónico en redes eléctricas donde no se posean equipos específicos que entreguen esta importante información

La serie de Fourier de una señal o función periódica x(t) tiene la siguiente expresión:
 

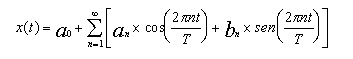
ecuación 1

donde

T: período de la función
n: orden de la armónica
ao: valor medio de la función
an, bn : coeficientes de las series (magnitudes de las armónicas)

El vector armónico correspondiente se puede asociar con un módulo An y ángulo de fase (Fi)n de la siguiente manera:  

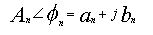
ecuación 2

donde la magnitud y el ángulo de fase vienen dados por:
 

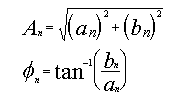
ecuación 3

Los coeficientes de Fourier se calculan mediante las siguientes expresiones:
 

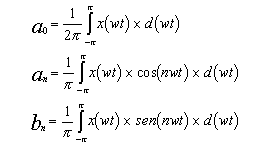
ecuación 4

Considerando la frecuencia f en [Hz] y la frecuencia angular w en [rad/s], definida por:
 

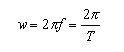
ecuación 5

Ejemplo: Análisis de Fourier de una señal cuadrada

Volver entrada